夏普大于4的策略有多恐怖?但它为什么好得不真实?
最后更新: 2025-11-27
Table of Content

学员问题: 我在交易领域的机器学习方面还是新手,一直在测试不同的预处理步骤来学习。其中一个模型突然表现得远好于我之前构建的任何模型,而唯一的主要变化是我如何对数据进行标准化(z-score 与 minmax 与 L2)。我确实很困惑,一个简单的标准化调整为何能产生如此大的差异,这里会有什么问题吗?
这是他的回测报告:
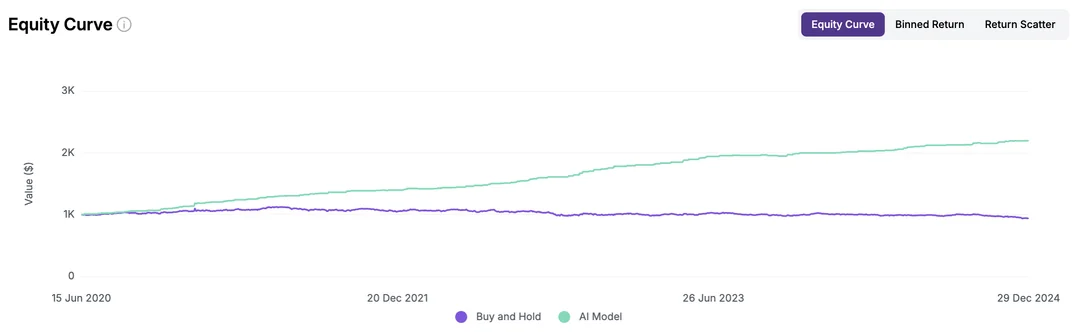

从这个报告中其实看不出来任何问题。但正如华尔街那句老话所说:“如果一个策略看起来好得令人难以置信,那它通常就是假的。” (If it looks too good to be true, it probably is.)
要分析问题,还得从底层开始。
首先一个简单的判断准则,任何人拿到 SR 大于4的结果,一般可以直接认为策略中引入了未来数据(Look-ahead Bias)。为什么这么说?因为夏普比率大于4的话,相当于年化超过200%了,因此这个数据是过于理想了。
Tip
取决于如何模拟数据。请见下一节。
夏普与年化收益的关系研究¶
这是网上比较难直接搜索出来答案的一个问题。所以,在这里我也分享一下研究方法。核心是要使用蒙特卡洛方法,先模拟出日收益分布,然后根据这个收益分布,分别计算年化收益和夏普比率。
因为收益分布是随机的,所以,由此计算出来的年化收益和夏普比率,也是随机的。但是,如果我们把这个过程重复非常多次,就能得到两者关系之间的稳定的分布。
首先,我们要根据投资品种,模拟出合理的日收益分布。我们以 A 股为例,一个合理的分布是中心位于1e-3,scale 为0.03的正态分布(偏乐观)。
这是我们模拟出来的日收益分布:
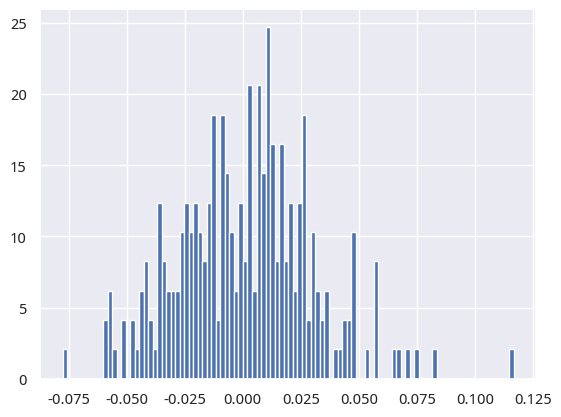
基于这些模拟的收益数据,我们就可以绘制出年化收益与夏普比率之间的关系,如下图所示:
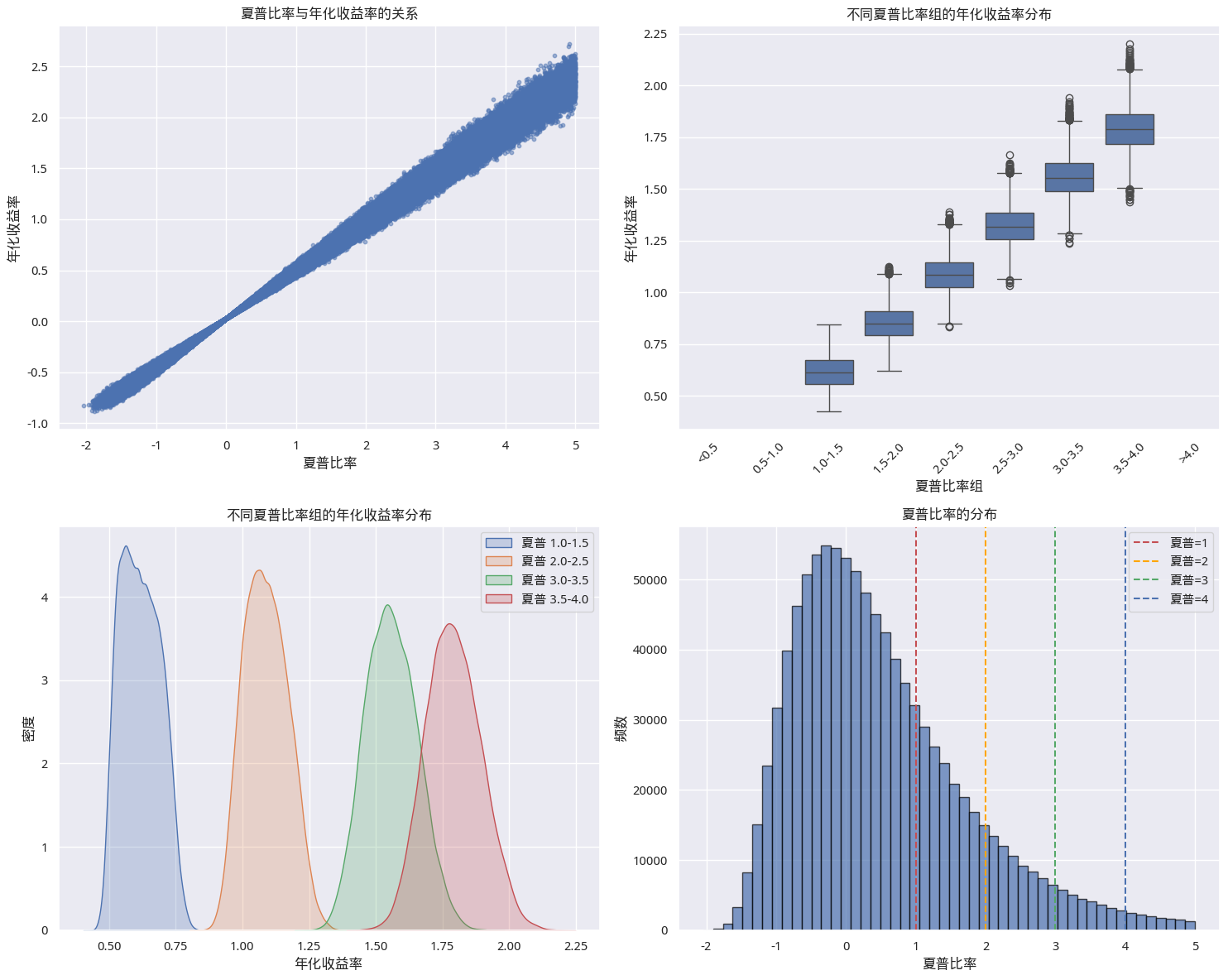
也许你会认为,日收益均值设置为0,scale 设置为0.02更合理。在这种情况下(更低的波动),如果策略的夏普达到了4,那么,年化收益的中位数值会是120%,仍然是过于优秀了。
因此,当我们看到夏普大于4时,几乎可以『毫不怀疑』地『怀疑』策略中引入了未来数据。
未来数据是如何引入的?¶
当我们使用统计方法时,一定要注意使用的数据的时间范围。这也是量化回测中最著名的陷阱之一:前视偏差(Look-ahead Bias)。
提问学员的问题是,他在使用 z-score 的时候,是用整个回测期间的数据进行 z-score 化的,而不是使用的截止到回测当天之前的数据进行 z-score 化的。
上帝视角的均值回归¶
当我们在整个回测期间使用 z-score 化的数据时,就引入了未来数据。如果回测发生在 [start, end] 期间,那么很有可能在 [start, t] 期间的数据分布是与 [start, end] 期间数据分布不一致的。
想象一下,你正在根据布林带(Bollinger Bands)进行交易,这本质上就是一种动态的 Z-Score 策略。如果你在 2020 年初计算 Z-Score 时,使用了包含 2020 年 3 月美股熔断期间的剧烈波动数据来计算全局标准差(Standard Deviation),会发生什么?
全局标准差会被熔断期间的极端波动拉大。因此,在熔断发生前的正常波动期间,你的模型计算出的 Z-Score 会比实际值更小(因为分母变大了)。这意味着模型会认为市场处于“异常平静”的状态,或者价格没有偏离均值太远。而在熔断发生时,由于你已经“预知”了这种波动是全局分布的一部分,模型可能会在市场恐慌时表现得异常镇定,甚至精准抄底。
这就是为什么学员的策略收益变得非常好——他的模型开了“上帝视角”,提前知道了整个考试期间的答案分布。
为什么 Min-Max 归一化更危险?¶
如果我们来看 minmax 归一化可能引起的错误,问题就会更容易理解。这个问题在股票和加密货币市场上更显著,因为理论上股票和加密货币的走势并不是零中心对称的随机游走,前者是按照国家的 GDP增长的相关函数增长的;后者因为是通缩货币,所以增长是通缩率的反比函数。
如果这些理论很枯燥和难懂,那么我们只要记住一个相关的结论,股价是可以涨到天上去的。但如果你使用 [start, end] 区间的数据进行 min-max 归一化,那么,就相当于在 [start, t] 区间里,看到了当时还没有涨上去的 max(close[start, end])。
如果你使用的是机器学习模型,那么多数情况下,它是无法在 [start, t] 的区间内,预测出来一个 [start, end] 区间中才存在的最大值的。这种归一化实际上是在告诉模型:“现在的价格相对于未来见过的最高价来说,还很便宜,赶紧买!”
正确的做法:滚动窗口¶
为了避免这种自我欺骗,我们必须严格遵守时间点(Point-in-Time)原则。在 t 时刻进行标准化时,只能使用 t 时刻之前的数据。
业界通用的做法是使用滚动窗口(Rolling Window)或扩展窗口(Expanding Window)进行标准化:
- 滚动窗口:例如,只使用过去 250 天的数据来计算均值和标准差,用于当天的 Z-Score 标准化。这模拟了真实的移动平均线逻辑。
- 扩展窗口:使用从回测开始到昨天的所有数据来计算统计量。
虽然这样做可能会导致模型表现“变差”,但这才是你能拿回家的真实收益。毕竟,我们在赚取 alpha 的路上,首先要战胜的不是市场,而是我们自己想走捷径的人性。
题图来自Dmytro Yarish@unsplash