tools »

前后复权都不对，动态复权又太贵！一文揭示策略失败的根本原因

#polars   #pandas   #numpy   #滑动窗口  

最后更新: 2025-11-24

---

Table of Content

对股价数据进行复权是一个基本的概念，你可能已经知道，存在前复权和后复权两种基本的复权方式，此外，还有动态前复权。但是，你上过的量化课可能只教过你如何计算这几种复权；而没有告诉你，它们将如何影响你的策略。

简言之，动态前复权是最贴近实盘的复权方式，它在回测的每一个时间点上，都完美地复现了当时看到的最真实的价格；就像策略投入实盘之后会看到的那样。

但是，动态前复权并不意味着仅仅对成交价进行复权。你有没有想过，如果没有对使用的因子进行相应的复权，你的策略将会如何表现呢？

什么是动态前复权

动态前复权就是在回测的每一个时间点 T1, T2, ..., Tn 上，都独立进行前复权。它相当于下面的伪码：

for i in range(len(prices)):
    qfq(prices[:i])

很多回测框架并不支持动态前复权。比如，在 backtrader 中，一般我们要在策略初始化时，就把行情数据添加为数据源，并且进行复权。然后，可以调用 backtrader 的指标体系，计算策略指标；也可能引入自己的因子。其它框架的情况也与此类似。

最后，在 next 方法中，框架把数据传递给我们，此时得到的因子与行情数据都是基于复权后的数据来计算的。

问题是，像 backtrader 这样的框架中，采用的复权都是静态的，即基于整个回测期间的某一个固定时间点来进行复权的；如果是前复权，则是基于最后一天的复权因子向前复权；如果是后复权，则是基于第一天的复权因子向后复权。这样会使用在回测到时间点 t 时，看到的数据和指标与实盘中是不一样的（即，假设你曾在过去的某个时间点 t 也对这支股票进行了研究，那么，当时你计算出来的指标，与回测时，价格经过静态复权后，再计算出来的指标，就是不一样的）。

如果我们在 next 方法中，自己进行前复权呢？此时当然就是动态前复权了，它完美地复现了当时的实盘环境。但是，动态前复权在实现上，就会遇到性能挑战。

在上面的伪码中，复权过程被调用 len(prices)次, 每次传入的价格序列长度随时间展开，依次递增；而静态前复权则只相当于调用了一次qfq(prices)。考虑到现代 CPU 的并行计算能力，后者的速度将远超前者。

不仅如此，在对价格进行动态前复权之后，我们还需要对因子也进行动态前复权。由于前复权的特性，历史数据无法复用（因此，基于前复权的因子数据存入数据库是没有意义的），只能推翻掉，完全重新计算。考虑到因子的数据巨大，计算量又比较复杂，这样就导致了严重的性能问题。

不过，在深入讨论动态前复权的性能问题之前，我们先来看看，基于动态前复权来计算因子，真的是有必要的吗？

因子为何也要动态前复权？

斜率因子(slope)是各类动量策略中的常用因子。它的计算原理是，将价格进行滑动窗口，计算窗口内价格序列的斜率。我们就以它为例来说明因子动态复权的必要性。

如果在不同的复权方式下，因子的数值能保持一致，那么，我们就不需要动态前复权了。反之，我们就证明了动态前复权的必要。

下面的代码将分别计算出前复权、后复权、动态前复权下，各期的 slope 值。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

random.seed(42)
pct_change = np.random.normal(0, scale=0.02, size=200)
price = np.cumprod(1 + pct_change).round(2)

# 生成不严格单调递增的序列，它的 cumprod 就会是一个比较好的复权因子样本
f = np.array(random.sample([0, 0.01, 0.02], counts=[130, 50, 20], k = 200))
adjust = (1 + f).cumprod()
adjust[:10]

# 统一的斜率因子计算函数
def slope(ts, win):
    x = np.arange(len(ts))
    y = ts
    coef = np.polyfit(x, y, 1)
    return coef[0]

def slope_with_static_qfq(prices, adjust, win): 
    # 对整个价格序列进行前复权
    qfq_prices = price * adjust / adjust[-1]
    slopes = [slope(qfq_prices[i-win:i], win) for i in range(win, len(price))]
    return np.array(slopes)

def slope_with_hfq(prices, adjust, win):
    # 对整个价格序列进行后复权
    hfq_prices = price * adjust / adjust[0]
    slopes = np.array([slope(hfq_prices[i-win:i], win) for i in range(win, len(price))])
    return np.array(slopes)

# 计算动态前复权下的斜率，这也是我们在实盘中，真正看到的斜率
def slope_with_dyn_qfq(prices, adjust, win):
    slopes = []
    for i in range(win, len(prices)):
        ts = prices[i-win:i] * adjust[i-win:i] / adjust[i]
        s = slope(ts, win)
        slopes.append(s)

    return np.array(slopes)

df = pd.DataFrame({
    "static_qfq": slope_with_static_qfq(price, adjust, 5),
    "static_hfq": slope_with_hfq(price, adjust, 5),
    "dyn_qfq": slope_with_dyn_qfq(price, adjust, 5),
}, index=range(5, len(price)))

df.plot()
df.describe()

最终的输出会是三条曲线：

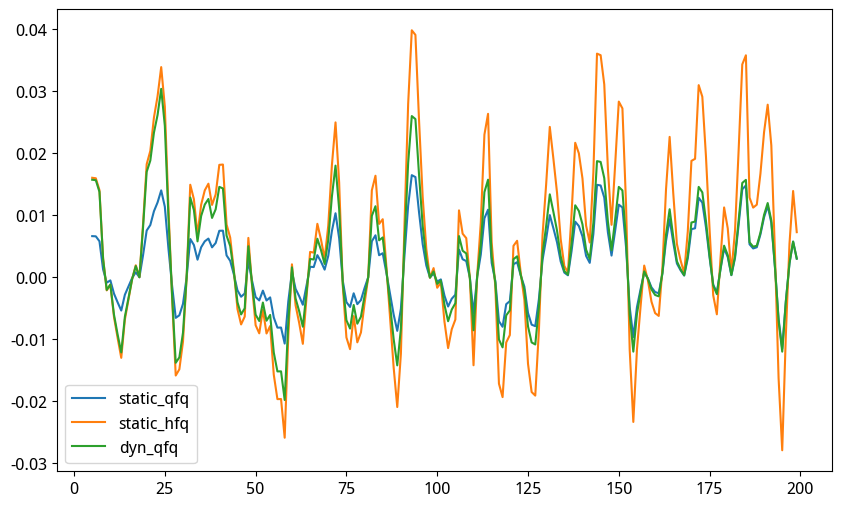
你发现问题了吗？

因为『真相』只有一个！但是我们却得到了三个！这正是问题！

与惟一的真实值（动态前复权）相比，后复权放大了斜率的波动，前复权缩小了斜率的波动。如果我们把时间拉得更长一点，就更能看出前后复权因子的荒谬性：

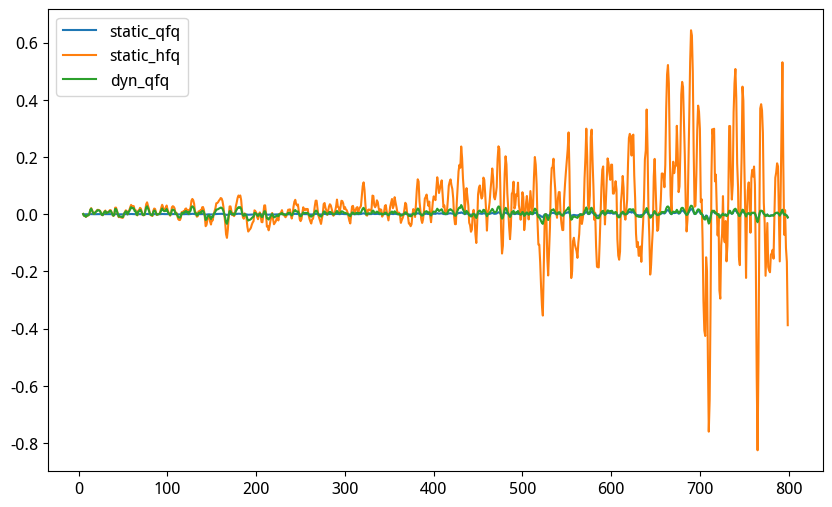
在这个图中，随着时间的推移，后复权的斜率波动越来越大。而越往前推，前复权的斜率波动就越来越小。这意味着什么？

我们分别取200， 400和800期的斜率因子，统计它们的波动率，得到下表：

	static_qfq	static_hfq	dyn_qfq
200	0.86%	2.09%	1.12%
400	0.39%	2.33%	0.69%
800	0.38%	13.55%	1.01%

很显然，只有动态前复权的波动率基本不随统计周期改变，而统计周期越长，后复权 slope 因子的波动率就越高；前复权因子的波动率就越小。

这说明，这两种模式下的 slope 因子都不是时间平稳的。对一个非时间平稳的因子，实际上是无法使用它的统计特性的。

只有基于动态前复权，我们才能说，过去十年里，每当斜率大于 x 时，股价就会上涨多少；而当斜率小于 x时，股价就会下跌多少。如果我们使用其它两种方式计算出来的斜率因子，没有任何一种方法可以学习到它们与收益之间的关系。

但是，如果因子也必须基于动态前复权数据来构造的话，这样因子库就会失效（因为存储量巨大）；而在运行时实时计算，无论是回测，还是实盘，都会面临极大的计算压力。

有没有更好的解决方案呢？

性能陷阱与优雅的解决方案

答案是肯定的，只不过，我们需要把因子的计算分成两步。第一步的结果可以存入因子库；尽管它还不是动态前复权的因子，但是，只需要经过很简单的快速计算，就可以转换成为动态前复权的因子。

这里我们先做一点数学推导，以证明这种方法的可行情。我们还是以斜率因子为例。

对于前复权的因子，它的计算公式是：

\[ Slope = Cov(X, P')/Var(X) \tag 1 \]

这是 P'是在时间 \(T_0\)到 \(T_t\)期间的前复权价格。X 是range(0, t) 的序列。由前复权计算公式：

\[ P' = P * adjust/adjust_{[-1]} \tag 2 \]

代入1)式，得到第t 期的动态前复权斜率因子：

\[ \begin{align} Slope_t &= Cov(X, P * adjust/adjust_{[-1]}) / Var(X) \tag 3 \\ &= \frac{1}{adjust_{[-1]}}Cov(X, P * adjust) / Var(X) \tag 4 \\ &= \frac{1}{adjust_{[-1]}}Cov(X, P * \frac{adjust}{adjust_0} * adjust_0) / Var(x) \tag 5 \\ &= \frac{adjust_{0}}{adjust_{[-1]}}Cov(X, P * adjust/adjust_0) / Var(X) \tag 6 \\ &= \frac{adjust_{0}}{adjust_{[-1]}}Slope_{hfq} \tag 7 \\ \end{align} \]

其中 $$ Cov(X, P * adjust/adjust_0) / Var(X) \tag 8 $$

是后复权计算公式。

由此，我们就建立了斜率因子在后复权与动态前复权之间的桥梁。注意7）中，对于任意一个时刻 t，\(adjust_0\)都是一个常量，是我们回测起始时间时的复权因子；而\(adjust_[-1]\)则是 t 时刻的复权因子。

因此，每一期的动态前复权 slope，就等于后复权 slope 因子乘以\(adjust_0/adjust\)。式子中的 adjust 是复权向量，包含了从回测起始时间到当前时间t的所有复权因子。

由此，我们就得到了一个在性能上与静态复权相当的动态前复权因子计算方案。它只比静态复权多了n (n等于回测周期）个乘法操作，这一点时间是可以忽略不计的。

现在，我们来验证一下上述推导过程是否正确。如果公式是正确的，那么，我们就可以这样计算出动态前复权：

from numpy.testing import assert_array_almost_equal
# 计算后复权因子
hfq_slope = slope_with_hfq(price, adjust, 5)

# 调整为动态前复权
actual = hfq_slope * adjust[0] / adjust[5:]
expect = slope_with_dyn_qfq(price, adjust, 5)

assert_array_almost_equal(actual, expect, decimal=5)

验证通过！

是不是所有的因子，都可以先计算后复权因子，再乘以 adjust[0]/adjust[t]，得到动态前复权因子？

常见因子调整公式

不同的因子调整方法是不一样的。

1. 移动平均（Moving Average, MA）

\[ \begin{align} MA_{dyn}(t) &= Mean(P') \\ &= Mean(P * adj/adj_{t}) \\ &= Mean(P * adj/adj_0 * adj_0/adj_{t}) \\ &= \frac{adj_0}{adj_{t}}Mean(P * adj/adj_0) \\ &= \frac{adj_0}{adj_{t}}MA_{hfq}(t) \\ \end{align} \]

所以，要计算基于动态前复权的移动平均因子，也只需要先计算出基于基准复权的序列，再求移动平均（基于基准复权），最后将它除以\(\frac{adj_0}{adj_{t}}\)即可。

2. 波动率（Volatility, StdDev）

\[ \begin{align} Vol_{dyn}(t) &= \text{Std}(P') && \text{(1. 定义动态波动率)} \\ &= \text{Std}(P \cdot adj / adj_{t}) && \text{(2. 代入价格定义)} \\ &= \frac{1}{adj_{t}} \text{Std}(P \cdot adj) && \text{(3. 提出常数因子)} \\ &= \frac{1}{adj_{t}} \text{Std}\left(\frac{P \cdot adj}{adj_0} \cdot adj_0\right) && \text{(4. 引入基准复权因子)} \\ &= \frac{adj_0}{adj_{t}} \text{Std}\left(\frac{P \cdot adj}{adj_0}\right) && \text{(5. 再次提出常数因子)} \\ &= \frac{adj_0}{adj_{t}} \text{Std}(P_{hfq}) && \text{(6. 识别出后复权价格)} \\ &= \frac{adj_0}{adj_{t}} Vol_{hfq}(t) && \text{(7. 识别出后复权波动率)} \end{align} \]

调整方式跟移动平均一样。如果是以方差作为因子呢？那么调整系数则是 \((adj_0/adj_{t})^2\)。

3. 无量纲因子

一些无量纲因子，比如 RSI,布林带，它们可以基于静态复权数据进行计算，一般无须额外调整。一般地，如果一个因子是基于价格涨跌幅计算的，那么，它已经消除了复权方式的影响，所以，我们就不必要对它进行动态复权了。

实际上，对于斜率因子，注意它受绝对价格的影响，因此不同品种之间的斜率差异较大，不具有可比性。所以，实际上要进行截面上的斜率因子比较，我们应该对价格进行某种去量纲化（比如除以 price_0），得到相对价格，再来计算斜率。此时，斜率因子就变成了一个无量纲因子，不仅可以跨品种比较，而且也不需要进行动态复权的调整了。

综合以上讨论，能否使用两步法来计算动态前复权因子，关键取决于因子计算函数的齐次性。如果因子计算函数是一次刘性的，则调整因子与 ma/slope 一样；二次齐性的，则与方差一样；无量纲因子则是零次齐性的，无须调整。

如果是因子计算是非齐次函数，比如 MACD，此时是无法通过两步法来计算动态前复权因子的。如果因子计算函数中使用了对数，那么调整算法将是加法而非乘法。

所以，具体如何调整，要在分析因子计算函数的数学特性后才能确定。

拯救你的因子库

基于以上讨论，我们得到几个重要结论：

1. 小心使用基于静态复权方法计算出来的因子库。这样计算出来的因子库有可能不具有时间平稳特性，因此我们无法寻找和利用其统计规律。
2. 如果因子计算函数是复权因子的齐次函数，则可以使用两步法来快速计算动态前复权因子，并且因子可以存入数据库。
3. 两步法是向量化运算，步骤是：
4. 通过价格序列（比如收盘价）与复权因子相乘，得到基准复权价序列（也可以存后复权价格）
5. 通过1）中计算的价格序列，计算各种因子的中间值并存数据库。
6. 在需要动态前复权的时候，根据2的结果，乘以调整系数，即可得到动态前复权因子。

看过这篇文章，快去检查一下你所使用的量化框架吧。它的因子库构建正确吗？当你质疑因子的有效性时，其实是不是因为因子计算方法的问题？

如果你想要转入量化行业，或者正在做量化，但还没建立起清晰的量化图景，往往是因为你还没有系统地接受过量化课程训练。我们为你准备了《量化二十四课》和《因子分析与机器学习策略》等多门量化课程，帮你快速、深入打牢量化基础！